Finite-state machine

A finite-state machine (FSM) or finite-state automaton (plural: automata), or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states. The machine is in only one state at a time; the state it is in at any given time is called the current state. It can change from one state to another when initiated by a triggering event or condition, this is called a transition. A particular FSM is defined by a list of the possible states it can transition to from each state, and the triggering condition for each transition.

Finite-state machines can model a large number of problems, among which are electronic design automation, communication protocol design, parsing and other engineering applications. In biology and artificial intelligence research, state machines or hierarchies of state machines are sometimes used to describe neurological systems and in linguistics—to describe the grammars of natural languages.

Concepts and vocabulary

A state describes a behavioral node of the system in which it is waiting for a trigger to execute a transition. Typically a state is introduced when the system does not react the same way to the same trigger. In the example of a car radio system, when listening to the radio (in the radio state), the "next" stimulus means going to the next station. But when the system is in the CD state, the "next" stimulus means going to the next track. The same stimulus triggers different actions depending on the current state. In some Finite-state machine representations, it is also possible to associate actions to a state:

Entry action: which is performed when entering the state,
Exit action: which is performed when exiting the state.

A transition is a set of actions to be executed when a condition is fulfilled or when an event is received.

Representations

For an introduction, see State diagram.

State/Event table

Several state transition table types are used. The most common representation is shown below: the combination of current state (e.g. B) and input (e.g. Y) shows the next state (e.g. C). The complete actions information is not directly described in the table. Which can be added only using footnotes. An FSM definition including the full actions information is possible using state tables (see also VFSM).

State transition table
Current state → Input ↓	State A	State B	State C
Input X	...	...	...
Input Y	...	State C	...
Input Z	...	...	...

UML state machines

The Unified Modeling Language has a notation for describing state machines. UML state machines overcome the limitations of traditional finite state machines while retaining their main benefits. UML state machines introduce the new concepts of hierarchically nested states and orthogonal regions, while extending the notion of actions. UML state machines have the characteristics of both Mealy machines and Moore machines. They support actions that depend on both the state of the system and the triggering event, as in Mealy machines, as well as entry and exit actions, which are associated with states rather than transitions, as in Moore machines.

SDL state machines

The Specification and Description Language is a standard from ITU and is one of the best languages to describe state machines because it includes graphical symbols to describe actions in the transition:

send an event
receive an event
start a timer
cancel a timer
start another concurrent state machine
decision

SDL embeds basic data types called Abstract Data Types, an action language, and an execution semantic in order to make the finite state machine executable.

Other state diagrams

There are a large number of variants to represent an FSM such as the one in figure 3.

Usage

In addition to their use in modeling reactive systems presented here, finite state automata are significant in many different areas, including electrical engineering, linguistics, computer science, philosophy, biology, mathematics, and logic. Finite state machines are a class of automata studied in automata theory and the theory of computation. In computer science, finite state machines are widely used in modeling of application behavior, design of hardware digital systems, software engineering, compilers, network protocols, and the study of computation and languages.

Classification

There are two different groups of state machines: Acceptors/Recognizers and Transducers.

Acceptors and recognizers

Acceptors and recognizers (also sequence detectors) produce a binary output, saying either yes or no to answer whether the input is accepted by the machine or not. All states of the FSM are said to be either accepting or not accepting. At the time when all input is processed, if the current state is an accepting state, the input is accepted; otherwise it is rejected. As a rule the input are symbols (characters); actions are not used. The example in figure 4 shows a finite state machine which accepts the word "nice". In this FSM the only accepting state is number 7.

The machine can also be described as defining a language, which would contain every word accepted by the machine but none of the rejected ones; we say then that the language is accepted by the machine. By definition, the languages accepted by FSMs are the regular languages—that is, a language is regular if there is some FSM that accepts it.

Start state

The start state is usually shown drawn with an arrow "pointing at it from any where" (Sipser (2006) p. 34).

Accept (or final) states

Accept states (also referred to as accepting or final states) are those at which the machine reports that the input string, as processed so far, is a member of the language it accepts. It is usually represented by a double circle.

An example of an accepting state appears in the diagram to the right: a deterministic finite automaton (DFA) that detects whether the binary input string contains an even number of 0's.

S₁ (which is also the start state) indicates the state at which an even number of 0's has been input. S₁ is therefore an accepting state. This machine will finish in an accept state, if the binary string contains an even number of 0's (including any binary string containing no 0's). Examples of strings accepted by this DFA are epsilon (the empty string), 1, 11, 11..., 00, 010, 1010, 10110, etc...

Transducers

Transducers generate output based on a given input and/or a state using actions. They are used for control applications and in the field of computational linguistics. Here two types are distinguished:

Moore machine: The FSM uses only entry actions, i.e., output depends only on the state. The advantage of the Moore model is a simplification of the behaviour. Consider an elevator door. The state machine recognizes two commands: "command_open" and "command_close" which trigger state changes. The entry action (E:) in state "Opening" starts a motor opening the door, the entry action in state "Closing" starts a motor in the other direction closing the door. States "Opened" and "Closed" stop the motor when fully opened or closed. They signal to the outside world (e.g., to other state machines) the situation: "door is open" or "door is closed".

Mealy machine: The FSM uses only input actions, i.e., output depends on input and state. The use of a Mealy FSM leads often to a reduction of the number of states. The example in figure 7 shows a Mealy FSM implementing the same behaviour as in the Moore example (the behaviour depends on the implemented FSM execution model and will work, e.g., for virtual FSM but not for event driven FSM). There are two input actions (I:): "start motor to close the door if command_close arrives" and "start motor in the other direction to open the door if command_open arrives". The "opening" and "closing" intermediate states are not shown.

In practice^{[of what?]} mixed models are often used.

More details about the differences and usage of Moore and Mealy models, including an executable example, can be found in the external technical note "Moore or Mealy model?"

Determinism

A further distinction is between deterministic (DFA) and non-deterministic (NFA, GNFA) automata. In deterministic automata, every state has exactly one transition for each possible input. In non-deterministic automata, an input can lead to one, more than one or no transition for a given state. This distinction is relevant in practice, but not in theory, as there exists an algorithm (the powerset construction) which can transform any NFA into a more complex DFA with identical functionality.

The FSM with only one state is called a combinatorial FSM and uses only input actions. This concept is useful in cases where a number of FSM are required to work together, and where it is convenient to consider a purely combinatorial part as a form of FSM to suit the design tools.

Alternative semantics

There are other sets of semantics available to represent state machines. For example, there are tools for modeling and designing logic for embedded controllers.^[1] They combine hierarchical state machines, flow graphs, and truth tables into one language, resulting in a different formalism and set of semantics.^[2] Figure 8 illustrates this mix of state machines and flow graphs with a set of states to represent the state of a stopwatch and a flow graph to control the ticks of the watch. These charts, like Harel's original state machines,^[3] support hierarchically nested states, orthogonal regions, state actions, and transition actions.^[4]

FSM logic

The next state and output of an FSM is a function of the input and of the current state. The FSM logic is shown in Figure 8.

Mathematical model

In accordance with the general classification, the following formal definitions are found:

A deterministic finite state machine or acceptor deterministic finite state machine is a quintuple 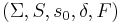, where:
- $\Sigma$ is the input alphabet (a finite, non-empty set of symbols).
- $S$ is a finite, non-empty set of states.
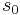- $s_0$ is an initial state, an element of $S$ .
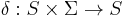- $\delta$ is the state-transition function: $\delta: S \times \Sigma \rightarrow S$ (in a nondeterministic finite automaton it would be 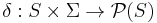$\delta: S \times \Sigma \rightarrow \mathcal{P}(S)$ , i.e., $\delta$ would return a set of states).
- $F$ is the set of final states, a (possibly empty) subset of $S$ .

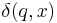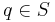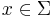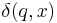For both deterministic and non-deterministic FSMs, it is conventional to allow $\delta$ to be a partial function, i.e. $\delta(q,x)$ does not have to be defined for every combination of $q \isin S$ and $x \isin \Sigma$ . If an FSM $M$ is in a state $q$ , the next symbol is $x$ and $\delta(q,x)$ is not defined, then $M$ can announce an error (i.e. reject the input). This is useful in definitions of general state machines, but less useful when transforming the machine. Some algorithms in their default form may require total functions.

A finite-state machine is a restricted Turing machine where the head can only perform "read" operations, and always moves from left to right.^[5]

A finite state transducer is a sextuple 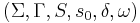, where:
- $\Sigma$ is the input alphabet (a finite non empty set of symbols).
- $\Gamma$ is the output alphabet (a finite, non-empty set of symbols).
- $S$ is a finite, non-empty set of states.
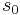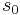- $s_0$ is the initial state, an element of $S$ . In a nondeterministic finite automaton, $s_0$ is a set of initial states.
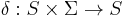- $\delta$ is the state-transition function: $\delta: S \times \Sigma \rightarrow S$ .
- $\omega$ is the output function.

If the output function is a function of a state and input alphabet (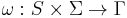 $\omega: S \times \Sigma \rightarrow \Gamma$ ) that definition corresponds to the Mealy model, and can be modelled as a Mealy machine. If the output function depends only on a state ( 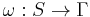$\omega: S \rightarrow \Gamma$ ) that definition corresponds to the Moore model, and can be modelled as a Moore machine. A finite-state machine with no output function at all is known as a semiautomaton or transition system.

If we disregard the first output symbol of a Moore machine, 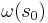$\omega (s_0)$ , then it can be readily converted to an output-equivalent Mealy machine by setting the output function of every Mealy transition (i.e. labeling every edge) with the output symbol given of the destination Moore state. The converse transformation is less straightforward because a Mealy machine state may have different output labels on its incoming transitions (edges). Every such state needs to be split in multiple Moore machine states, one for every incident output symbol.^[6]

Optimization

Main article: DFA minimization

Optimizing an means finding the machine with the minimum number of states that performs the same function. The fastest known algorithm doing this is the Hopcroft minimization algorithm.^[7]^[8] Other techniques include using an implication table, or the Moore reduction procedure. Additionally, acyclic FSAs can be minimized in linear time Revuz (1992) ^[9].

Implementation

Hardware applications

In a digital circuit, an FSM may be built using a programmable logic device, a programmable logic controller, logic gates and flip flops or relays. More specifically, a hardware implementation requires a register to store state variables, a block of combinational logic which determines the state transition, and a second block of combinational logic that determines the output of an FSM. One of the classic hardware implementations is the Richards controller.

Mealy and Moore machines produce logic with asynchronous output, because there is a propagation delay between the flip-flop and output. This causes slower operating frequencies in FSM. A Mealy or Moore machine can be convertible to a FSM which output is directly from a flip-flop, which makes the FSM run at higher frequencies. This kind of FSM is sometimes called Medvedev FSM.^[10] A counter is the simplest form of this kind of FSM.

Software applications

The following concepts are commonly used to build software applications with finite state machines:

References

^ Tiwari, A. (2002). Formal Semantics and Analysis Methods for Simulink Stateflow Models.
^ Hamon, G. (2005). A Denotational Semantics for Stateflow. International Conference on Embedded Software (pp. 164–172). Jersey City, NJ: ACM.
^ Harel, D. (1987). A Visual Formalism for Complex Systems. Science of Computer Programming , 231–274.
^ Alur, R., Kanade, A., Ramesh, S., & Shashidhar, K. C. (2008). Symbolic analysis for improving simulation coverage of Simulink/Stateflow models. Internation Conference on Embedded Software (pp. 89–98). Atlanta, GA: ACM.
^ Black, Paul E (12 May 2008). "Finite State Machine". Dictionary of Algorithms and Data Structures (U.S. National Institute of Standards and Technology). http://www.nist.gov/dads/HTML/finiteStateMachine.html.
^ James Andrew Anderson; Thomas J. Head (2006). Automata theory with modern applications. Cambridge University Press. pp. 105–108. ISBN 9780521848879. http://books.google.com/books?id=ikS8BLdLDxIC&pg=PA105.
^ Hopcroft, John E (1971). An n log n algorithm for minimizing states in a finite automaton [1]
^ Almeida, Marco; Moreira, Nelma; Reis, Rogerio (2007). On the performance of automata minimization algorithms. [2]
^ Revuz D. Minimization of Acyclic automata in Linear Time. Theoretical Computer Science 92 (1992) 181-189 181 Elsevier
^ "FSM: Medvedev". http://www.vhdl-online.de/tutorial/deutsch/ct_226.htm.

External links

Free On-Line Dictionary of Computing description of Finite State Machines
NIST Dictionary of Algorithms and Data Structures description of Finite State Machines

Automata theory: formal languages and formal grammars

Chomsky hierarchy

Type-0

—

Type-1

—

—

—

Type-2

—

—

Type-3

—

Grammars

Unrestricted

(no common name)

Context-sensitive

Indexed

Linear context-free rewriting systems etc.

Tree-adjoining etc.

Context-free

Deterministic context-free

Visibly pushdown

Regular

—

Languages

Recursively enumerable

Recursive

Context-sensitive

Indexed

Mildly context-sensitive

Tree-adjoining

Context-free

Deterministic context-free

Visibly pushdown

Regular

Star-free

Minimal automaton

Turing machine

Decider

Linear-bounded

Nested stack

Thread automata

Embedded pushdown

Nondeterministic pushdown

Deterministic pushdown

Visibly pushdown

Finite

Counter-free (with aperiodic finite monoid)

Each category of languages is a proper subset of the category directly above it. - Any automaton and any grammar in each category has an equivalent automaton or grammar in the category directly above it.